Что такое погрешность взвешивания какими причинами она может быть вызвана
Содержание статьи
Погрешности измерений
Как известно, ни одну физическую величину, в том числе и массу тела, невозможно определить с абсолютной точностью. Всегда есть погрешность измерений.
Результат взвешивания есть в общем случайная величина, определяемая совокупностью ряда различных факторов:
- чувствительностью;
- постоянством показаний весов;
- правильностью установки весов;
- температурными условиями, при которых проводили взвешивание;
- опытом работника, выполнявшего взвешивание;
- рядом других факторов.
Поэтому массу груза всегда определяют с какой-то погрешностью.
Погрешность измерений
Погрешность измерений — алгебраическая разность между полученным при измерении и действительным значениями измеряемой величины.
Погрешность результата измерения может быть представлена по-разному. Если ее выражают в тех же единицах, что и измеряемую величину, погрешность называют абсолютной.
Однако по величине абсолютной погрешности трудно судить о точности выполненного измерения. Этого недостатка лишен второй способ выражения погрешности результата измерения — в ее долях (или процентах).
Погрешность, выраженную таким способом, называют относительной. Все погрешности измерений можно разделить на систематические и случайные.
Они в большей или меньшей степени сказываются на результатах взвешивания. Чтобы знать, с какой точностью выполнено измерение, уметь исключать некоторые погрешности из результатов измерений, а влияние других снизить до минимума, необходимо разбираться в погрешностях, сопутствующих взвешиванию, и причинах, их вызвавших.
Систематическая погрешность измерений
Это постоянная по величине и знаку или переменная, изменяющаяся по определенному закону при повторных измерениях одной и той же величины, погрешность.
Систематическая погрешность входит в любой результат, несмотря на число повторных взвешиваний данного груза.
По виду причины, вызвавшей ту или иную систематическую погрешность при взвешивании, выделяют погрешность:
- обусловленную неправильной установкой и сборкой весов;
- возникшую из-за неравенства плеч коромысла, рычагов и т. д.;
- связанную с недостаточно точной подгонкой массы гирь;
- вызванную непостоянством температуры, при которой выполняли взвешивание;
- обусловленную действием аэростатической силы, если взвешивание выполняли в воздушной среде, и т. д.
Все перечисленные причины можно предвидеть и тем самым свести их влияние до минимума или полностью исключить из результата взвешивания.
Однако даже полностью исключив систематическую погрешность, нельзя добиться точного совпадения результатов многократного взвешивания одного и того же груза, так как любому измерению сопутствуют случайные погрешности.
Случайная погрешность
Она изменяется случайным образом при повторных измерениях одной и той же величины. Случайная погрешность не может быть полностью исключена из результатов взвешивания.
Однако сказанное не относится ко всей совокупности случайных погрешностей, возникающих при том или ином измерении. Выполняя ряд повторных взвешиваний, при помощи теории вероятностей и математической статистики можно несколько уточнить результат измерения, т. е. найти значение измеряемой величины, более близкое к истинному по сравнению с результатом одного измерения.
Промахи и грубые погрешности
Причинами, вызывающими промахи, могут быть:
- неправильный отсчет показаний стрелки;
- неправильная оценка цены деления шкалы;
- неверная запись результата;
- преждевременный или запоздалый отсчет;
- сдвиг или сотрясение весов, не замеченные наблюдателем, и т. д.
Однако, не все результаты взвешивания, которые значительно отличаются от других, можно характеризовать как промахи. Поэтому значительный интерес представляют способы выявления промахов.
Источник
Метрологические характеристики весов: погрешность, дискретность и классы точности
В практике измерения массы применяется разнообразные приборы и устройства, которые отличаются назначением, областью применением, принципом работы. В данное время на рынке весового оборудования число конструктивных модификаций весов исчисляется тысячами.
В 21 веке используются в основном электронные весы, но также на практике еще изредка применяются механические, а именно рычажные и даже пружинные весы.
Электронные весы подразделяются по принципу взвешивания на:
- Весы для статического взвешивания – весы платформенные, весы автомобильные, вагонные весы, товарные весы и лабораторные аналитические и прецизионные.
- Весы для взвешивания в движении – весы автомобильные подкладные, вагонные весы статико-динамические, весы вагонные динамические.
- Весы автоматические беспрерывного действия для суммарного учета – конвейерные весы и чеквейеры.
- Весы дискретного действия для суммарного учета автоматические – бункерные весы, автоматические весы-дозаторы и другие.
Погрешность весов при взвешивании
Для того, чтобы разобраться, что же такое погрешность весов при взвешивании, немного нужно окунуться в метрологическую терминологию.
Погрешность измерения — это отклонение результата измерения от истинного значения измеряемой физической величины, обозначение ∆.
∆ = х – х ист
Результат измерения – найденное значения физической величины опытным путем с использованием специальных технических средств, обозначение х.
Истинное значение физической величины – значение физической величины, которое идеальным образом в количественном и качественном отношении отражало бы соответствующее свойство объекта измерения, обозначение х ист.
Физическая величина – свойство, в качественном отношении характерна для многих объектов, явлений или процессов, но в количественном отношении индивидуальное для каждого из них.
В зависимости от выбранной классификационной характеристики существуют различные классификации погрешностей измерения, среди которых можно выделить наиболее распространенные:
- по форме выражения;
- по источникам возникновения;
- по закономерностям возникновения и проявления
По форме выражения погрешности делятся на абсолютные и относительные.
Абсолютная погрешность
Абсолютная погрешность весов – разность между результатом измерения массы груза на весах и истинным значением массы данного груза. Абсолютная погрешность по значению равна погрешности измерения и равна
∆ = х – х ист .
Относительная погрешность другие виды погрешностей
Относительная погрешность весов– это отношение абсолютной погрешности весов к условно истинному значению измеряемой величины, то есть к условно истинному значению массы груза, взвешиваемого на весах. Относительная погрешность равна:
где δ – относительная погрешность;
Δ – абсолютная погрешность;
– истинное значение физической величины – истинное значение массы взвешиваемого груза.
Основная погрешность (абсолютная, относительная) весов – это погрешность весов, определенная при нормальных условиях. Нормальные условия(i) – совокупность нормированных рабочих условий, которые устанавливаются для обеспечения достоверности взаимного сравнения результатов измерений. Нормированные рабочие(i) условия – условия эксплуатации, устанавливающие диапазон значений влияющих величин, при которых метрологические характеристики весов находятся в пределах нормированных максимально допустимых погрешностей.
Нормированные рабочие условия имеют такие показатели:
– диапазон температур от минус 10 ºС до плюс 40 ºС;
– относительная влажность – 98 % при температуре 25 ºС.
Дополнительные погрешности весов
Дополнительная погрешность –погрешность весов, которая дополнительно возникает при эксплуатации весов в условиях отклонения хотя бы одной из влияющих величин от нормированного значения.
По источникам возникновения погрешности измерения бывают инструментальные, методические и личные (погрешности оператора).
Инструментальная погрешность весов – составляющая погрешности измерения, обусловленная свойствами средства измерительной техники, в данном случае весов.
Методическая погрешность – составляющая погрешности измерения, обусловленная несовершенством метода измерения или несоответствием объекта измерения его модели, принятой для измерения.
Погрешность оператора – составляющая погрешности измерения, обусловленная индивидуальными свойствами оператора/весовщика.
По закономерностям возникновения и проявления различают систематические, случайные и чрезмерные погрешности.
Систематическая погрешность весов – составляющая общей погрешности измерения, остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины.
Случайная погрешность весов – составляющая общей погрешности измерения, меняется случайным образом (как по знаку, так и по величине) при повторных измерениях одной и той же величины.
Чрезмерная погрешность – погрешность измерения, которая существенно превышает ожидаемую при данных условиях погрешность.
Погрешность весов имеет свои пределы допустимых значений, которые регламентируются нормативным документом – стандартом. Результат значения измеряемой массы груза на весах в пределах допустимых погрешностей весов является приемлемым.
Также есть термин «предел допустимой погрешности»(i), вот его значение:
предел допустимой погрешности – это самая большая разница, положительная или отрицательная, установленная нормативным документом – стандартом между показанием весов и соответствующим действительным значением рабочих эталонов мер массы (гирь) при условии, что весы находятся в исходном положении и до нагрузки грузом имели нулевые показания.
Дискретность весов – цена действительного деления весов
Дискретность весов – это значение, выраженное в единицах массы, равное:
– разнице между значениями двух последовательных отметок шкалы – для аналогового отображения измеряемого значения массы;
или
– разнице между значениями двух последовательно отраженных показаний – для цифрового отображения измеряемого значения массы.
Дискретность весов обозначается, как d.
Цена поверочного деления весов
Цена поверочного деления – значение, выраженное в единицах массы, используемой для классификации, оценки соответствия, поверки весов(ссылка). Цена поверочного деления весов обозначается, как e.
Классы точности весов
Класс точности – обобщенная метрологическая характеристика, определяется границами основной и дополнительной погрешностей весов, а также другими метрологическими характеристиками весов.
Классы точности устанавливают в процессе проектирования весов с учетом проведенных испытаний в ходе проведения оценки соответствия требованиям Технического регламента, под действие которого попадают весы. Если в нормативном документе, Техническом регламенте, стандарте, или технических условиях, регламентирующего технические требования к весам конкретного типа, установлено несколько классов точности, то класс точности конкретных весов допускается присваивать при выпуске из производства и проведению испытаний на соответствие метрологическим характеристикам. А также понижать класс точности возможно по результатам периодической поверки (или другого вида поверки) в порядке, предусмотренном действующей методикой поверки данного типа весов.
Класс точности весов для статического взвешивания
Неавтоматические взвешивающие устройства, а именно весы для статического взвешивания: платформенные весы, железнодорожные весы, автомобильные весы, которые используются в законодательно регулируемой метрологии, попадают под действие Технічного регламенту щодо неавтоматичних зважувальних приладів и должны отвечать требованиям стандарта ДСТУ EN 45501 «Метрологічні аспекти неавтоматичних зважувальних приладів».
Весы квалифицируют в соответствии с:
– ценой поверочного деления e шкалы весов, которая отражает абсолютную точность;
– количеством поверочных делений n шкалы, которая отражает относительную точность.
Максимально допустимые погрешности выражают через значение цены поверочного деления e.
Более подробно о количестве поверочных делений n. Количество поверочных делений n – это отношение значения максимальной нагрузки Max весов до значения цены поверочного деления. Зная максимальную нагрузку Max весов и цену поверочного деления e шкалы весов можно высчитать количество поверочных делений n :
n = Max / e
Согласно ДСТУ EN 45501 весы для статического взвешивания подразделяются на такие классы точности:
– специальный класс точности I
– высокий класс точности II
– средний класс точности III
– обычный класс точности IIII
Цена поверочного деления e, количество поверочных делений шкалы n и минимальную нагрузку Min в соответствии с классом точности весов для статического взвешивания приведены в таблице 1.
Таблица 1.
| Класс точности весов для статического взвешивания | Цена поверочного деления шкалы, e | Количество поверочных делений, n = Мах / е | Минимальную нагрузка, Min (нижняя граница | |
| минимальное | максимальное | |||
| Специальний (І) | 0,001 г ≤ е a) | 50 000 | – | 100 е |
| Высокий (ІІ) | 0,001 г ≤ е ≤ 0,05 г | 100 | 100 000 | 20 е |
| 0,1 г ≤ е | 5 000 | 100 000 | 50 е | |
| Средний (ІІІ) | 0,1 г ≤ е ≤ 2 г | 100 | 10 000 | 20 е |
| 5 г ≤ е | 500 | 10 000 | 20 е | |
| Обычный (ІІІІ) | 5 г ≤ е | 100 | 1 000 | 10 е |
| a) Обычно невозможно выполнить испытания или поверку весов с е <1 мг из-за неопределенности испытательных нагрузок (в span) | ||||
Класс точности весов для динамического взвешивания
Для динамического взвешивания есть также разнообразные типы весов.
Класс точности весов для динамического взвешивания обозначается цифрами:
0,2 0,5 1 2
Например, класс точности 0,5 подразумевает, что:
Рассмотрим для наглядности
весы вагонные для динамического взвешивания
, которые используются в законодательно регулируемой метрологии, попадают под действие Технічного регламенту засобів вимірювальної техніки и отвечают требованиям стандарта ДСТУ OIML R 106-1 «Ваги залізничні платформні автоматичні. Частина 1 . Загальні технічні вимоги. Методи випробування».
Согласно ДСТУ OIML R 106-1 вагонные весы для динамического взвешивания подразделяются на 4 класса точности, более подробно в Таблице 2.
Таблица 2
| Класс точности | Процент от значения массы одного вагона или всего поезда | |
| при проведении оценки соответствия, периодической поверке | во время эксплуатации | |
| 0,2 | ± 0,10 % | ± 0,2 % |
| 0,5 | ± 0,25 % | ± 0,5 % |
| 1 | ± 0,50 % | ± 1,0 % |
| 2 | ± 1,00 % | ± 2,0 % |
При взвешивании вагона
Предел допускаемой погрешности во время взвешивания в движении сцепленных или расцепленных вагонов должен соответствовать наибольшему из следующих значений:
а) значению, вычисленному по таблице 2 и округленном до ближайшего значения, кратного цене деления шкалы е
b) значению, вычисленному по таблице 2 для массы отдельного вагона, которая составляет до 35% от наибольшего значения массы вагона, и округленном до ближайшего значения, кратного цене деления шкалы или
c) 1 d.
Пример взвешивания вагона для весов вагонных динамического взвешивания 2-го класса точности:
Масса контрольного вагона = 100 т
Наибольшая масса вагона Max = 100 т
Цена деления шкалы е = 0,2 т
Предел допустимой погрешности в соответствии с пунктом:
Таблица 2 пункт a) 1% · 100 т = 1 т;
Таблица 2 пункт b) 35% от Max · 100 т = 35 т, следующим образом:
1% = 0,35 т или 0,4 т (округленное значение) для 90% (54 из 60) контрольных вагонов;
2% = 0,7 т для 10% (6 из 60) контрольных вагонов;
Таблица 2 пункт c) 1 d = 0,2 т;
При взвешивании поезда
Предел допускаемой погрешности во время взвешивания в движении поезда должен соответствовать наибольшему из следующих значений:
а) значению, вычисленному по таблице 2 и округленном до ближайшего значения, кратного цене деления шкалы е
b) значению, вычисленному по таблице 2 для массы отдельного вагона, которая составляет до 35% от наибольшего значения массы вагона, умноженного на количество контрольных вагонов этого поезда (не более 10 вагонов) и округленном до ближайшего значения, кратного цене деления шкалы е
или
c) 1 d для каждого вагона данного поезда, но не более 10 d.
Пример взвешивания поезда для весов вагонных для динамического взвешивания класса точности 1:
Количество вагонов в поезде = 50
Количество контрольных вагонов в поезде = 15
Масса контрольного вагона = 100 т
Наибольшая масса вагона Max = 100 т
Цена деления шкалы е = 0,2 т
Предел допускаемой погрешности соответствии с пунктом:
Таблица 2 пункт a) 0,5% · 100 т · 15 контрольных вагонов = 7,5 т;
Таблица 2 пункт b) 35% Max · 10 контрольных вагонов = 350 т
0,5% · 350 т = 1,75 т, значение округляется до ближайшей погрешности шкалы
Таблица 2 пункт c) 1 d · 10 контрольных вагонов = 2 т.
Вывод
Рассмотрев такие метрологические характеристики весов, как погрешность, дискретность – действительная цена деления, цена поверочного деления и класс точности, видно, что эти характеристики взаимозависимы друг от друга и при изменении одной из характеристик, меняется тип весов. Со значением «тип весов» можно ознакомится в следующей статье.
Источник
Базовые метрологические понятия о весах
Дискретность:
d (цена деления) — это наименьшее значение, на которое изменяется показание дисплея электронных весов.
Пример: Например, если дисплей весов показывает вес 1 кг, то при добавлении груза весом 3 г показания будут равны 1,005 кг, т.е. будут меняться с дискретностью d = 5 г. Многие ошибочно полагают, что эта величина d и является погрешностью измерения веса. Однако это не так.
Погрешность или цена поверочного деления
е — это условная величина, выраженная в единицах массы и предназначенная для расчета погрешности весов. Значение е должно удовлетворять одному из следующих требований: — для весов специального (I) и высокого (II) класса точности е=2d, e=5d, e=10d — Для весов специального класса точности, у которых е не более 0,1 мг, допускаются следующие значения: е=20d, e=50d, e=100d е=200d, e=500d, e=1000d, где d — дискретность (цена деления).
Наибольший предел взвешивания (НПВ)
НПВ это верхняя граница предела взвешивания. НПВ определяет самую большую массу при взвешивании на весах за один раз.
Наименьший предел взвешивания (НмПВ)
НмПВ Очень важно знать, от какого наименьшего предела взвешивания производитель гарантирует указанную в руководстве по эксплуатации погрешность весов. Знать наименьший предел взвешивания принципиально важно, т.к. весы индицируют вес на дисплее даже в случае, если измеряемый вес меньше НмПВ, однако достоверными эти показания считать нельзя.
Класс точности
С 01.07.2001 г. вступил в действие новый ГОСТ 24104-2001 (взамен ГОСТ 24104-1988). Этот ГОСТ разработан на основе международных рекомендаций OIML и подразделяет весы на 3 класса точности:
- I специальный класс точности весов
- II высокий класс точности
- III средний
Калибровка и поверка
Это процедура регулировки цены деления весов.
Часто путают калибровку с поверкой весов. Поверка осуществляется, как правило, раз в год независимыми метрологическим службами (ЦСМ). Поверку производят с целью определения и подтверждения соответствия весов установленным техническими требованиями (ГОСТов, ТУ )
Бывает так, что потребители «довольствуются» этим и не осуществляют калибровку весов, хотя процедура эта – ежедневная. Более того, чем выше класс точности весов, тем чаще придется их калибровать в течение дня.
Калибровка бывает следующих видов:
- Внешняя калибровка — это калибровка с помощью калибровочной гири. Номинал гири того или иного класса должен быть близок, а еще лучше равен НПВ весов. Это коренным образом влияет на точность показаний.
- Внутренняя — это калибровка с помощью встроенного в весы эталонного груза. Удобство внутренней калибровки очевидно. Достаточно нажать кнопку, и весы дальше сами выполняют все необходимые подстройки. Однако при прочих равных условиях такие весы дороже аналогичных с внешней калибровкой.
- Автоматическая — это разновидность внутренней калибровки, при которой калибровка весов происходит без участия оператора. Весы данного типа автоматически определяют необходимость и выполняют калибровку при изменении внешних условий (давление, влажность, температура). Кроме того, в некоторых моделях предусмотрена плановая калибровка по времени, задаваемым оператором.
Классы гирь
Также как и весы, калибровочные гири делятся на несколько классов. Если подходить упрощенно, то чаще всего для типичных весов, находящихся в современных лабораториях, используются гири:
- класс Е2 (для калибровки весов Специального (I) класса точности – как правило, аналитические весы с дискретностью 0,1 мг);
- класс F1 (для калибровки весов Высокого (II) класса точности);
- класс F2 (для калибровки весов Среднего (III) класса точности).
Разумеется, допускается использование гирь более высокого класса для калибровки весов более низкого класса.
Повторяемость или среднеквадратическое отклонение (СКО)
СКО основано на рассмотрении отклонений значений признака отдельных единиц совокупности от средней арифметической. СКО показывает, насколько в среднем колеблется величина признака у единиц исследуемой совокупности, и выражается в тех же единицах измерения, что и варианты.
Защита весов по IP
Чтобы охарактеризовать допустимые условия эксплуатации конкретного электротехнического оборудования, для него устанавливается т.н. класс защиты IP (International Protect). Он кодируется двухзначным (или трехзначным) числом, каждая из цифр которого указывает (по условленной шкале) степень допустимого внешнего воздействия на данное изделие. Название норматива имеет вид IP XY, где первая цифра X указывает степень защиты от пыли и поражения электрическим током, а вторая Y — от воды.
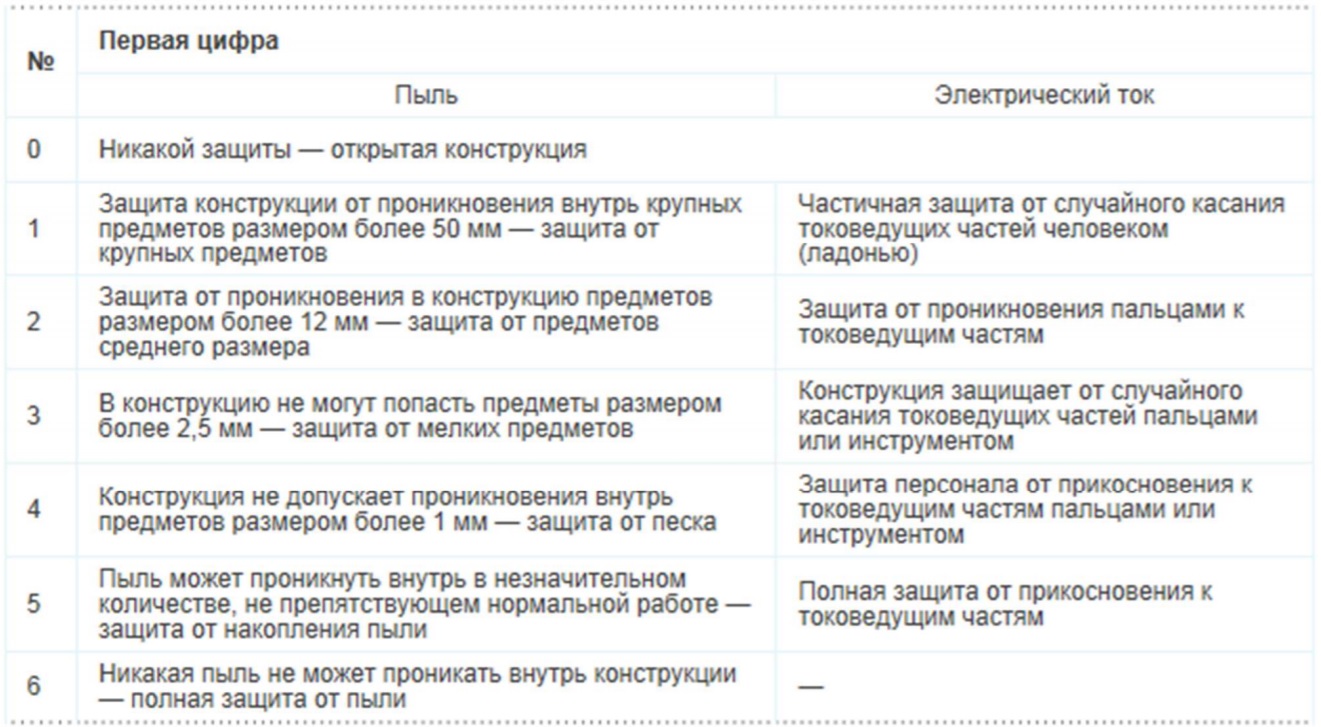

Источник